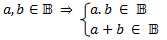É um método operacional que pode ser usado com vantagens para resolver equações diferenciais lineares. Pode-se converter funções comuns, tais como funções senoidais, funções senoidais amortecidas, funções exponenciais, enfim, uma função no domínio do tempo f(t) em uma função de uma variável complexa. Trata-se da mesma função vista de duas formas diferentes. Operações como diferenciação e integração podem ser substituídas por operações algébricas no plano complexo. O método da Transformada de Laplace permite o uso de técnicas gráficas para prever o desempenho do sistema sem a necessidade de resolver as equações diferenciais.
Uma variável complexa s tem uma componente real σ e uma componente imaginária jω, ou s = σ + jω. Uma função complexa G(s), uma função de s, tem uma parte real e uma parte imaginária, ou G(s) = Gx + jGy, em que Gx e Gy são reais. Uma função complexa G(s) é dita analítica em uma região se G(s) e todas as suas derivadas existirem naquela região. A derivada de uma função analítica G(s) é dada por:
O valor da derivada é independente da escolha da trajetória de Δs. Pode-se mostrar que se as derivadas tomadas ao longo de duas trajetórias quaisquer, especificamente Δs = Δσ e Δs = jΔω, são iguais, então a derivada é única para qualquer outra trajetória Δs = Δσ + jΔω.
Para uma particular trajetória Δs = Δσ ( trajetória paralela ao eixo real):
Para uma particular trajetória Δs = jΔω ( trajetória paralela ao eixo imaginário):
Se estes valores são iguais, então:

E se são satisfeitas as chamadas
condições de Cauchy-Riemann:
Então a derivada de G(s) é determinada unicamente.
Pontos do planos s em que a função G(s) é analítica são chamados de
pontos ordinários, enquanto que pontos do plano s em que a função G(s) não é analítica são chamados de
pontos singulares. Pontos singulares em que a função G(s) ou suas derivadas se aproximam de infinito são chamados
pólos.
Se G(s) tende a infinito quando s tendo a -p e se a função
(n= 1,2,3 ...) tem um valor infinito não nulo em s=-p, então s=-p é chamado de pólo de ordem n. Se n=1, o pólo é chamado um pólo simples. Se n=2,3..., o pólo é chamado de pólo de segunda ordem, pólo de terceira ordem, etc. Pontos em que G(s) = 0 são chamados de zeros.
Transformada de Laplace
-
Definição
Seja uma função do tempo f(t) seccionalmente contínua e tal que f(t)=0 para t<0, então a sua transformada de Laplace, F(s), onde s é uma variável complexa, será dada por:
Para que uma função tenha Transformada de Laplace ela tem que ser
causal, isto é, f(t)=0 para t<0.
Exemplos
- Função Impulso (Delta de Dirac)


Pode-se provar que:

Propriedade do Deslocamentto

Transformada de Laplace da função impulso:

- Função Degrau Unitário ( 1(t) ou u(t))


Transformada de Laplace da função degrau unitário

- Função Rampa


Transformada de Laplace da função rampa:

- Função Exponencial


Transformada de Laplace da função exponencial:

Referências: - http://www.dt.fee.unicamp.br/~www/ea612/
- Ogata,K. Engenharia de Controle Moderno - Cap 2