O sistema binário é o sistema de numeração do computador digital, que tem apenas dois simbolos, B:{0,1}. Cada dígito binário (1 ou 0) é chamado de bit. E o grupo de 8 bits é chamado de byte.
- Contagem em Binário
Correspondência entre números na base dez e na base dois:
Decimal Binário
0 0
1 1
2 10
3 11
4 100
⁞ ⁞
9 1001
dez 1010
- Conversão de Binário para Decimal
Estamos acostumados aos números decimais, porém nunca paramos para pensar no que isso quer dizer. Por exemplo, o número 341 pode ser escrito em potências de 10 da seguinte maneira:

Portanto, um número na base dois funcionará de maneira análoga, por exemplo:

- Potências de 2

- Conversão de Decimal para Binário
- Método das Divisões Sucessivas:
Divide-se o número decimal sucessivamente por 2, sendo que o número binário será a leitura dos restos dessas divisões. Por exemplo, se quisermos representar o número 23 na base binária, faremos:
resto
23/2 = 11 1
11/2 = 5 1
5/2 = 2 1
2/2 = 1 0
1/2 = 0 1
A condição de parada é a divisão resultar em 0. O sentido de montagem é do último para o primeiro número, ou seja, 23 decimal é igual a 10111 binário.
- Representação de números racionais positivos
Os números fracionários decimais seguem exatamente o mesmo raciocínio dos inteiros, a única diferença será o expoente negativo nas potências de dez. Exemplo:
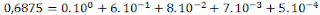
Então na base binária temos:

- Conversão de Decimal para Binário
- Método das Multiplicações Sucessivas
Multiplica-se a fração decimal por 2 e o número binário é coletado a partir da parte inteira do resultado. Nada melhor do que um exemplo:
0,6875x2 = 1,375
0,375x2 = 0,75
0,75x2 = 1,5
0,5x2 = 1,0 => condição de parada
Lendo na ordem direta dessa vez, temos então que 0,6875 decimal é 0,1011 binário.
- Bases Auxiliares
I - Base Hexadecimal
É uma base em que são usados 16 símbolos,
H: {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}
Decimal Hexadecimal Binário
0 0 0
1 1 1
2 2 2
⁞ ⁞ ⁞
10 A 1010
11 B 1011
12 C 1100
13 D 1101
14 E 1110
15 F 1111
- Conversão Binário para Hexadecimal
Como 16 é uma potência a quarta de 2, então cada 4 bits na base 2 serão 1 dígito na base 16. Exemplo:

- Conversão Hexadecimal para Binário
É a mesma ideia, basicamente convertemos elemento por elemento e com um pouco de prática fica fácil fazer cada passagem. Por exemplo, em F0CA em Hexadecimal será 1111000011001010 em binário.
1111 0000 1100 1010 (Binário)
F 0 C A (Hexadecimal)
15 0 12 10 (Decimal)
II - Base Octal
Utiliza 8 símbolos, O: {0,1,2,3,4,5,6,7}. Como 8=2³, então cada 3 bits correspondem a 1 dígito octal.
- Conversão de Octal para Binário
Completamente análogo ao Hexadecimal. Exemplo:

- Conversão Binário para Octal
Analisa-se o binário de 3 bits em 3 bits, completando com zero a esquerda se faltar bit. Exemplo 10110111, analisa-se:
111 = 7
110 = 6
010 = 2
Ou seja, 101110111 em binário é 267 em Octal.
