O Sistema Massa-Mola-Amortecedor

Equação Dinâmica

Isolando a segunda derivada

Colocando o sistema na forma de Espaço de Estados

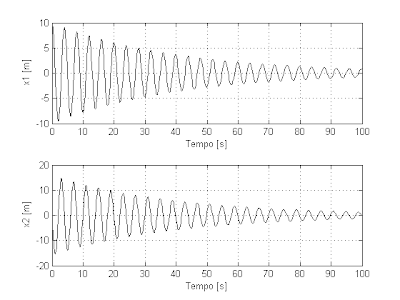
Em ambiente Matlab/Simulink e escolhendo m=2, b=0.1 e k=5, podemos verificar a resposta temporal da posição e da velocidade a uma entrada impulso:

Analisando esse sistema no Plano de Fases, isto é, plotando a resposta no espaço de estados, este formado por uma base de variáveis de estado, neste caso B=[x1,x2]. Obtemos:

Vemos que o sistema tende a posição de equilibrio no decorrer do tempo. A dissipação de energia no amortecedor é que provoca esse efeito. Temos que a energia potencial do sistema é sempre positiva e descresce ao longo do tempo, logo temos que a função da energia potencial V(x) é uma função de Lyapunov. Então o sistema é estável.

Podemos tirar essa mesma conclusão analisando sua Função de Transferência

Diagrama de Polos e Zeros

Pelo diagrama vemos que os polos do sistema estão do lado esquerdo do plano complexo. Isso caracteriza um sistema estável. Se pelo menos um polo tivesse do lado direito, o sistema seria instável. Além disso, vemos que os polos são complexos conjugados, caracterizando uma resposta temporal oscilatória. Se fosse estritamente real, sem parte complexa, a resposta seria exponencial.

Implementação no Matlab/Simulink

O Pêndulo Duplo

 

Simulação

Exemplos de resposta com diferentes condições iniciais

Considerando x1 a posição da primeiro pêndulo, x2 sua velocidade e x3 a posição do segundo pendulo e x4 sua velocidade:

a) Para x1(0)=1; x3(0)=0 :

b) Para x1(0)=1; x3(0)=1:

Fontes:
- http://en.wikipedia.org/wiki/Double_pendulum
- Vídeo do pêndulo duplo pode ser encontrado em http://www.poli.usp.br/d/pme2200/

Sistemas Dinâmicos Lineares - Parte II

Nos estudos de Controle, sempre nos utilizamos da entrada degrau para obter propriedades do sistema. Como a entrada a degrau é quase que uma entrada padrão, então é extremamente conveniente deduzir sua resposta temporal num sistema linear.

Como podemos notar, as respostas serão sempre caracterizadas por exponenciais. O que já muda em sistemas de segunda ordem, em que a uma entrada degrau, o sistema pode apresentar resposta oscilatória.

Circuito RC

Sistemas Dinâmicos Lineares - Parte I

São sistemas cuja dinâmica é representada por equações diferenciais de primeira ordem.
O engenheiro então fornece, através de seus conhecimentos, uma lei de controle possam cumprir certos objetivos de desempenho:

1. Erro estático: É o limite do erro para uma entrada. É razoável querer que o erro (e(t)) tenda a zero.
2. Tempo de subida (tr): Tempo em que a saída demorar para atingir (reach) 100% do seu valor final.
3. Tempo de assentamento (ts): É o instante de tempo em que o erro e(t) é menor do que um certo valor percentual escolhido pelo projetista, geralmente 2% ou 5%.
4. Máximo sobresinal (Mp): É o maior erro percentual em relação ao valor final.

Os principais problemas na vida de um engenheiro que trabalha com Controle, entre outras coisas, são fatores que atrapalham todo o projeto do controlador, tal qual:

• Complexidade do próprio controlador: Concerne na própria fabricação quanto sua complexidade matemática.
• Não linearidades em atuadores: Os atuadores podem apresentar comportamento não linear, cuja modelagem pode se tornar muito dificíl, até impossível se usar apenas o tratamento linear.
• Sinais de distúrbio: Os sinais de controle sofrem distúrbios, geralmente atrito e folgas. Por exemplo, numa modelagem de controle de uma embarcação, as ondas do mar entram como um distúrbio no sistema, já que são aleatórias e não previstas nas equações diferenciais. Por isso é necessário o conceito de robustez, ou seja, o sistema será controlado mesmo na presença de distúbios.
• Erros de modelagem: Como na grande maioria dos casos, faz-se aproximações da planta real, o que causa um erro de modelagem, que na verdade sempre estará presente em qualquer projeto real. Geralmente elimina-se os termos não lineares para fazer a simplificação do modelo.
• Ruído de medida: No uso de sensores, tem-se ruídos de alta frequência, atrapalhando na leitura e comprometendo a qualidade do controle.
  
  

A figura ilustra um típico sistema de controle em malha fechada. Esse tipo de malha é largamente utilizada, pois se tem a medida do erro, tanto quanto sua desejada redução.

Equação diferencial geral de um Sistema Linear de Primeira Ordem:

Em que y(t) e u(t) é a saída e a entrada do sistema respectivamente.

• Função de Transferência

Aplicando a Transformada de Laplace na Equação Diferencial, assumindo condições iniciais nulas:

• Polos e Zeros do Sistema
  
  

• Diagrama de Pólos e Zeros
  
  
  
   
• Ganho
  
  O ganho (g) é a relação entre o valor final da saída e o valor final da entrada, para qualquer tipo de entrada. É definida por:
  
                                            
  

Função de Transferência

Existem diversas formas de se representar o modelo de um sistema, tais como:

• Equações diferenciais de ordem n
• N equações diferenciais de ordem 1
• Função de Transferência (sistema linear)

Função de Transferência só é definida para equação diferencial linear. Se o modelo do sistema não for linear, é necessário linearizá-lo antes de tomar a função de transferência.

Seja um sistema descrito pela seguinte EDO de ordem n, sendo y(t) e u(t) a saída e a entrada, respectivamente.

Tem-se que n é maior ou igual a m. Aplicando a Transformada de Laplace na EDO, assumindo condições iniciais nulas:

G(s) é chamada de Função de Transferência do sistema.
Função de Transferência é a relação entre as transformadas de Laplace da saída e da entrada do sistema, considerando condições iniciais nulas.

Exemplo

Solução de Equações Diferenciais Ordinárias usando Transformada de Laplace

Uma das maiores vantagens, talvez a maior, é a facilidade com que podemos resolver equações diferenciais ordinárias usando a Transformada de Laplace. Para se fazer isso, segue-se o seguinte procedimento:

1. Aplica-se a transformada da equação diferencial ordinária, transformando-a de uma equação do tempo para uma equação em s.
2. Resolve-se a equação algébrica resultante, obtendo-se a transformada dessa variável.
3. Calcula-se algo chamado "Tranformada Inversa de Laplace", que é feita com muita simplicidade através da tabela, obtendo-se então a solução da equação diferencial.

 Exemplo