MecFlu from tadeuferreirajr
segunda-feira, 19 de dezembro de 2011
sexta-feira, 7 de outubro de 2011
Circuitos Analógicos
Aqui utilizarei o software Oregano do Linux para simular alguns componentes eletrônicos.
Primeiramente construirei um circuito simples, com um resistor e uma fonte de corrente alternada.
Primeiramente construirei um circuito simples, com um resistor e uma fonte de corrente alternada.
No segundo circuito, um diodo é introduzido, cortando a voltagem do semiciclo negativo.
Com o diodo no sentido contrário, a voltagem no semiciclo positivo é que fica cortada.
Colocando um capacitor em paralelo com a carga, temos uma retificação melhor do sinal, como segue:
quarta-feira, 21 de setembro de 2011
Controladores
- Controlador Liga-Desliga (ON-OFF)
Neste controlador, o elemento de atuação possui apenas dois estados. Sua aplicação se deve apenas à facilidade de construção e baixo custo. Dependendo do sinal do erro, a entrada fica na posição máxima ou mínima.
O segundo termo é mínimo e igual a zero ou o oposto do máximo. São geralmente implementados com válvular solenóides.
Seu símbolo em simuladores, por exemplo Matlab/Simulink é:
Exemplo: válvula. Uma válvula de um reservatório pode ser do tipo ON-OFF em que ela está aberta ou fechada. Assim o fluxo, variável controlada, é constante ou nula.
- Controlador Proporcional
Ação de Controle
- Controlador Integral
Função de Transferência
Se o valor do erro dobra, o valor de u(t) varia duas vezes mais rápido. Se o erro for zero, o valor de u(t) permanece estacionário.
- Controlador Proporcional-Integral (PI)
Função de Transferência
Kp é o ganho proporcional e Ti é o tempo integral. Para um sinal de erro na forma de degrau, o sinal de controle resulta numa reta.
- Controlador Proporcional-Derivativo (PD)
Função de Transferência
Diagrama de Blocos
Kp é o ganho proporcional e a constando Td é o tempo derivativo. Esse controle fornece uma ação de controle proporcional à derivada do erro. O tempo derivativo Td é o intervalo de tempo que a ação de controle derivativa antecede a ação de controle proporcional. Tem a vantagem de ser antecipatória, porém amplifica ruídos. Esse controlador jamais poderá ser usado isoladamente, pois se houver um erro no regime permanente, o sistema não será controlado, já que o controlador derivativo atua apenas em regimes transitórios.
- Controlador Proporcional- Integral-Derivativo (PID)
Função de Transferência
terça-feira, 9 de agosto de 2011
O Diodo
O elemento eletrônico não-linear mais simples e fundamental é o diodo. Ele possui dois terminais e guarda uma relação não-linear entre i (corrente) e v(voltagem). Sua aplicação mais comum é em retificação, ou seja, converter ac (alternating current = corrente alternada) em dc (direct current = corrente contínua).
Diodos são feitos de um substrato de material semicondutor, em geral um cristal de silício. Os cristais de silício, formados por ligações covalentes são isolantes, mas quando dopados (dopagem = inserção de átomos de outros elementos no substrato), podem conduzir corrente.
O Diodo Ideal
Seu símbolo está indicado em a) e sua característica i-v está mostrada em b). Dependendo do sentido da corrente, ele deixará passar ou não. Se o sentido da corrente for da anodo pro catodo, ele deixa passar, do contrário não. Uma pequena simulação mostra qual o sentido em que ele deixa passar e qual ele não deixa.
Como o led da primeira figura acendeu, então essa posição que o diodo deixa a corrente passar, a segunda figura é analogament oposta.
- O Retificador de Meia Onda
Tomemos um circuito simples em que a voltagem é alternada.
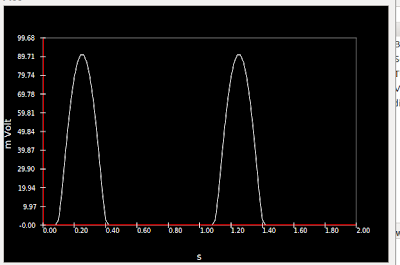
O diodo deixará passar apenas a parte positiva da voltagem da fonte, já que quando ela for negativa, a corrente tende a ter um sentido inverso do indicado na figura e o diodo não deixa passar. Então o resultado é uma voltagem sempre positiva, não alternando para valores negativos como antes.
- O Retificador de Onda Completa com Derivação Central
No semiciclo positivo, isto é, quando a onda da tensão é positiva, há passagem de corrente pelo diodo D1, enquanto o diodo D2 corta. No semiciclo negativo, isto é, quando a onda da tenção da linha é negativa, o diodo D2 conduz e o diodo D1 corta, assim se consegue uma voltagem na carga um pouco melhor que o retificador anterior. A forma de onda fica:
A tensão da linha é vs e a tensão resultante na carga é vo. Dá pra ver que no lugar em que antes era zero, agora tem um forma de onda, já sendo uma melhora na retificação do sinal.
- O Retificador de Onda Completa em Ponte
No semiciclo positivo D1 e D2 conduzem, enquanto D4 e D3 cortam. No semiciclo negativo D1 e D2 cortam, enquanto D3 e D4 conduzem. O resultado da onda é exatamente igual a anterior, já que é retificador de onda completa, o que difere é a forma de montagem, antes era derivação central e agora está na forma de ponte.
Até agora se utilizou apenas diodos para se obter um sinal constante a partir de um senoidal. A forma da onda resultante sempre foi positiva, mas ainda senoidal. Usando agora filtros, consegue-se uma mescla entre senoidal e exponecial, melhorando o resultado. Será usado o circuito RC como filtro. Veja neste mesmo blog na parte de simulações uma pequena análise sobre o circuito RC.
- O Retificador de Meia Onda com Filtro Capacitivo
Temos um retificador de meia onda e um capacitor em paralelo com a carga. Num primeiro momento o capacitor se carrega seguindo a voltagem da linha. Quando a tensão da linha fica menor que a tensão do capacitor, o diodo corta, pois haveria condução de corrente no sentido inverso, já que o capacitor se carregou e a tensão de linha está menor. Então temos a voltagem sendo acumulada na forma senoidal, tensão da linha, depois caindo na forma exponencial, descarregamento do capacitor.
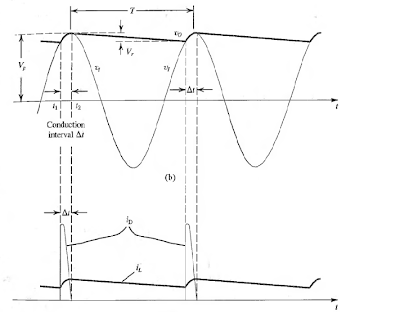
O restultado é:
Observa-se um sinal mais próximo de uma reta, que é o objetivo da retificação. O Vr da figura é chamado de ondulação, em inglês o "r" é de 'ripple'. O T é o período e o Vp é a tensão de pico. Veja que a tensão sobe senoidalmente de acordo com a linha, carregando o capacitor. Quando a onda desce, a tensão no capacitor é maior, ocasionando uma movimentação de corrente no sentido contrário, do capacitor pra linha, mas o diodo corta e não há essa condução, o que resta é simplesmente o descarregamento no capacitor já que não há mais alimentação nele. Esse descarregamento ocorre do capacitor para a carga. Até um ponto em que a tensão de linha volta a ser maior que a tensão do capacitor e o carrega novamente, repetindo o ciclo.
Quando maior o capacitor, mais lentamente ele se descarrega e menor a ondulação.
Fontes:
Foto inicial: http://www.betoeletronica.com.br/
Imagens retiradas do livro "Microelectronic Circuits", Sedra.
sexta-feira, 5 de agosto de 2011
Leis da Mecânica
As Leis de Newton
Leis magnas que explicam os movimentos dos corpos.
Transformação de um Sistema de Coordenadas
Toma-se dois sistemas de coordenadas distintos (S1,S2) e um ponto P.
Utiliza-se um lema importantíssimo do Cálculo Variacional que será a base para toda a evolução dos resultados.
Ou seja, a variação da velocidade angular é vista da mesma maneiro pelos dois sistemas de coordenadas. Colocando o vetor r, obtem-se:
Chega-se numa relação de velocidades, em que a velocidade absoluta é a velocidade do ponto P em relação ao sistema de coordenadas inicial, o S1. A velocidade relativa é a velocidade vista pelo sistema S2 e a velocidade de arrastamento é a velocidade de arrastamento é a velocidade do ponto P vista pelo S1 como se ele estivesse fixo no S2, sendo arrastado por este.
Como resultado tem-se que a aceleração no sistema absoluto é uma composição de acelerações: a aceleração em relação ao sistema relativo; a segunda e a terceira parcela formam a chamada aceleração de arrastamento e uma última parcela é a aceleração de Coriolis.
Dinâmica de um Sistema de n Pontos Materiais
Tomando um ponto de massa mi para análise, temos que a força aplicada nessa massa é a somatória vetorial das forças externas e das forças de interação com outras massas:
Da segunda Lei de Newton, temos que a variação do momento linear é igual à somatória das forças:
A partir disso podemos encontrar importantes resultados da Mecânica, por exemplo, integrando a equação:
Multiplicando ambos os lados por dr:
Momento Angular
Soma dos momentos da quantidade de movimento de cada partícula.
![[;\vec{H_{0}}=\displaystyle\sum\limits_{i=1}^n \vec{r_i} \times m_i\vec{v_i};]](http://thewe.net/tex/%5Cvec%7BH_%7B0%7D%7D=%5Cdisplaystyle%5Csum%5Climits_%7Bi=1%7D%5En%20%5Cvec%7Br_i%7D%20%5Ctimes%20m_i%5Cvec%7Bv_i%7D "\vec{H_{0}}=\displaystyle\sum\limits_{i=1}^n \vec{r_i} \times m_i\vec{v_i}")
Derivando,
![[;\frac{d}{dt}\vec{H_{0}}=\displaystyle\sum\limits_{i=1}^n \vec{r_i} \times \frac{d}{dt}m_i\vec{v_i};]](http://thewe.net/tex/%5Cfrac%7Bd%7D%7Bdt%7D%5Cvec%7BH_%7B0%7D%7D=%5Cdisplaystyle%5Csum%5Climits_%7Bi=1%7D%5En%20%5Cvec%7Br_i%7D%20%5Ctimes%20%5Cfrac%7Bd%7D%7Bdt%7Dm_i%5Cvec%7Bv_i%7D "\frac{d}{dt}\vec{H_{0}}=\displaystyle\sum\limits_{i=1}^n \vec{r_i} \times \frac{d}{dt}m_i\vec{v_i}")
![[;\frac{d}{dt}\vec{H_{0}}=\displaystyle\sum\limits_{i=1}^n \vec{r_i} \times \vec{F_i} + \displaystyle\sum\limits_{i=1}^n \vec{r_i} \times \displaystyle\sum\limits_{j=1}^n \vec{F_{ij}};]](http://thewe.net/tex/%5Cfrac%7Bd%7D%7Bdt%7D%5Cvec%7BH_%7B0%7D%7D=%5Cdisplaystyle%5Csum%5Climits_%7Bi=1%7D%5En%20%5Cvec%7Br_i%7D%20%5Ctimes%20%5Cvec%7BF_i%7D%20+%20%5Cdisplaystyle%5Csum%5Climits_%7Bi=1%7D%5En%20%5Cvec%7Br_i%7D%20%5Ctimes%20%5Cdisplaystyle%5Csum%5Climits_%7Bj=1%7D%5En%20%20%5Cvec%7BF_%7Bij%7D%7D "\frac{d}{dt}\vec{H_{0}}=\displaystyle\sum\limits_{i=1}^n \vec{r_i} \times \vec{F_i} + \displaystyle\sum\limits_{i=1}^n \vec{r_i} \times \displaystyle\sum\limits_{j=1}^n \vec{F_{ij}}")
![[;\frac{d}{dt}\vec{H_{0}}=\displaystyle\sum\limits_{i=1}^n \vec{r_i} \times \vec{F_i^e} + \displaystyle\sum\limits_{i=1}^n \displaystyle\sum\limits_{j=1}^n \vec{r_i} \times \vec{F_{ij}};]](http://thewe.net/tex/%5Cfrac%7Bd%7D%7Bdt%7D%5Cvec%7BH_%7B0%7D%7D=%5Cdisplaystyle%5Csum%5Climits_%7Bi=1%7D%5En%20%5Cvec%7Br_i%7D%20%5Ctimes%20%5Cvec%7BF_i%5Ee%7D%20+%20%5Cdisplaystyle%5Csum%5Climits_%7Bi=1%7D%5En%20%5Cdisplaystyle%5Csum%5Climits_%7Bj=1%7D%5En%20%5Cvec%7Br_i%7D%20%5Ctimes%20%5Cvec%7BF_%7Bij%7D%7D "\frac{d}{dt}\vec{H_{0}}=\displaystyle\sum\limits_{i=1}^n \vec{r_i} \times \vec{F_i^e} + \displaystyle\sum\limits_{i=1}^n \displaystyle\sum\limits_{j=1}^n \vec{r_i} \times \vec{F_{ij}}")
![[;\frac{d}{dt}\vec{H_{o}}=\vec{M_o^e};]](http://thewe.net/tex/%5Cfrac%7Bd%7D%7Bdt%7D%5Cvec%7BH_%7Bo%7D%7D=%5Cvec%7BM_o%5Ee%7D "\frac{d}{dt}\vec{H_{o}}=\vec{M_o^e}")
Referências:
- Mecânica Newtoniana, Lagrangiana & Hamiltoniana, João Barcelos Neto.
Leis magnas que explicam os movimentos dos corpos.
- Lex I: Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare
Uma partícula livre ou está em repouso ou em movimento retilíneo com velocidade constante.
- Lex II: Mutationem motis proportionalem esse vi motrici impressae, etfieri secundum lineam rectam qua vis illa imprimitur.
Quando uma partícula interage, a resultantes das forças que atuam sobre a partícula corresponde à variação de seu momento linear.
- Lex III: Actioni contrariam semper et aequalem esse reactionem: sine corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi.
Quando duas partículas interagem, a força numa delas possui o mesmo módulo, mesma direção e sentido contrário à força que atua na outra.
Transformação de um Sistema de Coordenadas
Toma-se dois sistemas de coordenadas distintos (S1,S2) e um ponto P.
Isto quer dizer: qualquer entidade vetorial "a" respeita esta relação, sendo os índices S1 e S2 correspondendo as referências indicadas. Nota-se que os dois sistemas de coordenadas S1 e S2 tem origem coincidente.
Escolhendo "a" como sendo o próprio "w", temos um resultado interessante:
Ou seja, a variação da velocidade angular é vista da mesma maneiro pelos dois sistemas de coordenadas. Colocando o vetor r, obtem-se:
Chega-se numa relação de velocidades, em que a velocidade absoluta é a velocidade do ponto P em relação ao sistema de coordenadas inicial, o S1. A velocidade relativa é a velocidade vista pelo sistema S2 e a velocidade de arrastamento é a velocidade de arrastamento é a velocidade do ponto P vista pelo S1 como se ele estivesse fixo no S2, sendo arrastado por este.
Escolhendo-se desta vez a própria velocidade absoluta no Lemma, tem-se:
Como resultado tem-se que a aceleração no sistema absoluto é uma composição de acelerações: a aceleração em relação ao sistema relativo; a segunda e a terceira parcela formam a chamada aceleração de arrastamento e uma última parcela é a aceleração de Coriolis.
Dinâmica de um Sistema de n Pontos Materiais
Tomando um ponto de massa mi para análise, temos que a força aplicada nessa massa é a somatória vetorial das forças externas e das forças de interação com outras massas:
Da segunda Lei de Newton, temos que a variação do momento linear é igual à somatória das forças:
Multiplicando ambos os lados por dr:
Momento Angular
Soma dos momentos da quantidade de movimento de cada partícula.
Derivando,
(Teorema do Momento Angular em relação a origem)
Referências:
- Mecânica Newtoniana, Lagrangiana & Hamiltoniana, João Barcelos Neto.
sábado, 9 de julho de 2011
O Sistema Massa-Mola-Amortecedor
Equação Dinâmica
Isolando a segunda derivada
Colocando o sistema na forma de Espaço de Estados
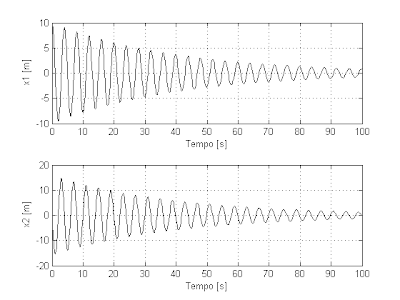
Em ambiente Matlab/Simulink e escolhendo m=2, b=0.1 e k=5, podemos verificar a resposta temporal da posição e da velocidade a uma entrada impulso:
Analisando esse sistema no Plano de Fases, isto é, plotando a resposta no espaço de estados, este formado por uma base de variáveis de estado, neste caso B=[x1,x2]. Obtemos:
Vemos que o sistema tende a posição de equilibrio no decorrer do tempo. A dissipação de energia no amortecedor é que provoca esse efeito. Temos que a energia potencial do sistema é sempre positiva e descresce ao longo do tempo, logo temos que a função da energia potencial V(x) é uma função de Lyapunov. Então o sistema é estável.
Podemos tirar essa mesma conclusão analisando sua Função de Transferência
Podemos tirar essa mesma conclusão analisando sua Função de Transferência
Diagrama de Polos e Zeros
Pelo diagrama vemos que os polos do sistema estão do lado esquerdo do plano complexo. Isso caracteriza um sistema estável. Se pelo menos um polo tivesse do lado direito, o sistema seria instável. Além disso, vemos que os polos são complexos conjugados, caracterizando uma resposta temporal oscilatória. Se fosse estritamente real, sem parte complexa, a resposta seria exponencial.
Implementação no Matlab/Simulink
Assinar:
Postagens (Atom)